📈 Session 2

Linear Regression with Neural Networks

This session we mainly focus on the training of a neural network. This will include:

Data preparation
Constructing a simple neural network
Training a model to fit the data

Links:

📈 Linear Regression

While many will likely remember what linear regression is from high school, it is good to remind ourselves again of the concept. To do so, let’s imagine a simple scenario:

Peter is a kid who gets $2 of pocket money a day.
Peter has been saving for a while and currently has $50 saved.
How much will Peter have in a week?

The answer of course should be $64. Anyone would be able to calculate this but let’s write it out in an official manner.

$money = 2*x + savings$

This can also be written out more generally for any linear formula in the following way:

$y = a*x+b$ which is the same as writing $y=ax+b$

$y = m*x + b$ which is the same as writing $y=mx+b$

Or in your case you might have learned this formula with a different set op characters in place of the variables. This formula is one that also makes a very common occurrence in many neural networks we see today. Often however this is written with a slightly different name for both the slope ($a$ or $m$) and the intercept ($b$) in the world of deep learning. We often referred to as the weight and bias, where the weight is the slope, and the bias is the intercept. Written out in a similar official manner it would look like the following:

$y=weight*x+bias$

$y=wx+b$

In this we’ll train a Neural Network to learn the $w$ and $b$.

So how would our data look like?

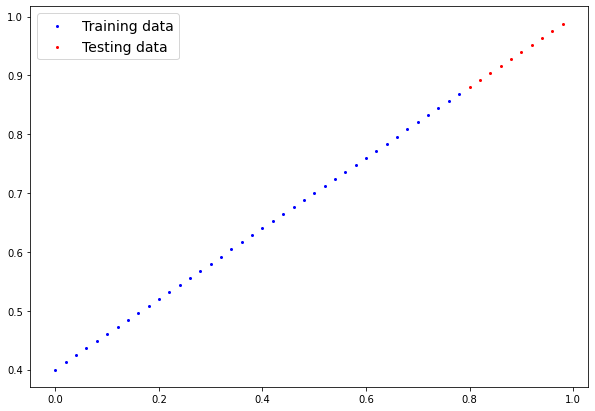
Linear Training data for a Neural Network — Figure 1: Training data for Linear regression

🔪 Data Splitting

Before we dive into the training of a neural network, it’s essential to delve deeper into how we handle our data. In machine learning, how we split our data plays a pivotal role in the effectiveness of our models. This process is not just a formality but a foundational step that significantly impacts the outcome of our training.

Why Split the Data?

The primary reason for splitting our data into at least two sets - usually training and testing sets - is to evaluate the model’s performance accurately. By training on one set of data and testing on a separate set, we can assess how well our model generalizes to new, unseen data. This helps to prevent overfitting, where the model performs exceptionally well on the training data but poorly on any new data.

Notes on types of machine learning

🧑‍🏫 Supervised Machine Learning

Supervised learning involves training a model on a dataset that includes both the input features and the corresponding target outputs (or labels). This in essesence means that the model learns by example. Through providing the model with inputs and outputs, the model is able to learn the relationsship that exists between the input and the output.

🤷 Unsupervised Machine Learning

Unsupervised machine learning does not rely on labeled data. Instead, it aims to identify inherent structures or patterns in the data without any guidance on what the output should be. This form of learning can be useful for clustering, dimensionality reduction, and discovering hidden features within the data. It’s essential to differentiate between the two as it affects how we prepare our data and the algorithms we use for analysis.

Dividing Data: Training and Test Sets

Once we have our data, the next step is to divide it into training and test sets. This division is crucial for evaluating the performance and generalizability of our model. Here’s how we typically approach this:

We can conceive of two scenarios you’ll likely see.

1. Imagine you want to classify images of art by their style. You have labelled many examples (supervised) and split the data as follows:

Training Set: This dataset is used to train our model. It’s like the textbook for the model, containing the examples from which it learns. Typically, we allocate around 70-80% of our total dataset to training.
Test Set: This dataset is used to test our model after it has been trained. It acts as an exam to see how well the model has learned from the training set. This data is thus unseen. Usually, 20-30% of the dataset is reserved for testing.

2. You are working on classifying the printshops of pages texts from Colonial Korea. You have many labelled examples of such pages. Yet you want to also see how the model would perform on ‘unseen’ data.

Simply dividing into train and test sets will not give you a proper test metric here. That is because pages of the same book look alike. If you randomly split it might catch up on other data that is not directly relevant. Often you might want to keep some texts apart in such a case and create a Train, Validation and Test set.

Training Set: ncludes a wide range of pages from different books to cover various printshop styles, with entire books or large sections grouped together. This method helps the model learn key features without overfitting to specific book layouts.
Validation Set: Features pages from books that could be in the training set but are kept separate to tune hyperparameters and model architecture. Like the training set, it groups whole books or large sections to challenge the model with realistic, unseen data.
Test Set: Contains pages from entirely new books, excluded from the training and validation sets, to evaluate the model’s final performance. This ensures the model is tested on completely unseen data from diverse printshops, providing a true test of its generalization ability.

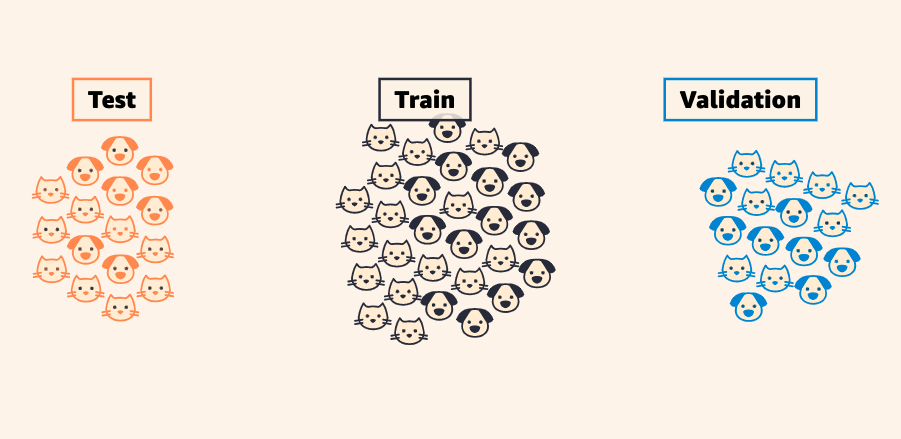
train-test-validation split — Figure 2: Visual representation of a 50/25/25 split

Image source: MLU

MLU has a great visual page showing visually the splitting of data!

The key is to ensure that the data is randomly split, maintaining a representative mix of the data characteristics in both sets. This way, we avoid bias in how the model learns and ultimately test its performance.

🧠 A linear neuron

Imagine a neuron as a tiny decision-making unit in a vast network of similar units, all working together to make sense of the information fed into the network.

Connections and Weights

Each neuron is connected to several other neurons or inputs. You can think of each connection as a bridge carrying information from one neuron to another. Now, not all information (or inputs) is equally important for the decision the neuron needs to make. This is where weights come into play.

A weight is a numerical value (think of it as a strength level) assigned to each connection that the neuron has with its inputs. It determines how much influence each input has on the neuron’s decision. If an input’s weight is high, it means that input plays a significant role in what the neuron decides to output. Conversely, a low weight means the input has less influence.

The Neuron and Its Bias

Now, onto the neuron itself. Apart from the inputs and their weights, a neuron has its own inherent property called bias. Think of the bias as the neuron’s own opinion or inclination, which it adds to the weighted inputs it receives. The bias allows the neuron to adjust its output further, making the model more flexible and capable of learning complex patterns.

On weights and biases

In the section on linear regression we have already seen the terms Weight and Bias. It is important to realize that in that section, they are the inherent properties of the data you have seen–the linear line. However in this section both are now parameters of a linear neuron. This neuron is made to model linearity and is thus very good at solving problems with linear data.

How It All Comes Together: A Linear Neuron

A linear neuron combines all the weighted inputs it receives, adds its bias, and then produces an output based on that combined information. This process can be visualized simply as:

Each input is multiplied by its corresponding weight.
All these weighted inputs are then added together.
The bias is added to this sum.

In essence, the linear neuron is making a weighted decision based on its inputs, influenced by its own bias, to produce an output. This output then serves as an input to other neurons or as part of the final output of the neural network, depending on where the neuron sits in the network’s architecture.

$\text{Output} = (\text{Input}_1 \times \text{Weight}_1) + (\text{Input}_2 \times \text{Weight}_2) + \ldots + \text{Bias}$

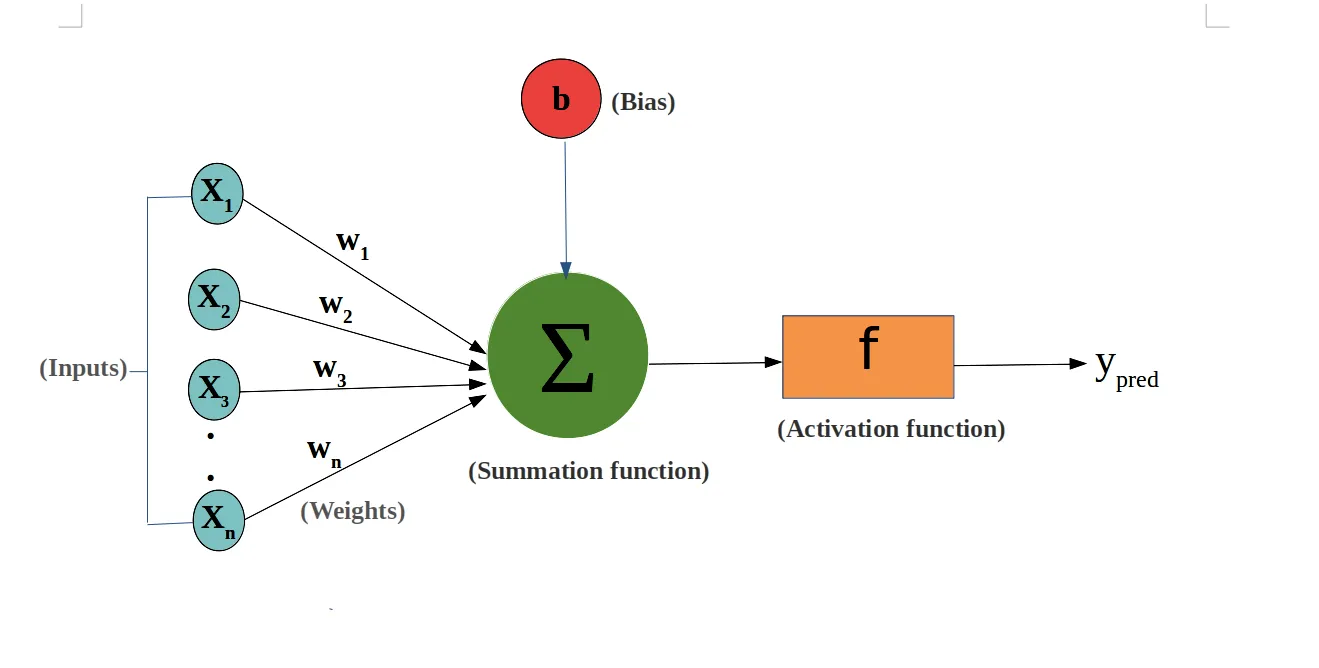
Please ignore the ‘Activation Function’ part until the next session where this will come into play. Image source

🔥 A network in PyTorch

Creating networks in Pytorch are done by creating a class object.

It would look like the following:

class LinearRegressionModel(nn.Module):
  def __init__(self):
    super().__init__()
    # below this come the layers
    self.linearlayer = nn.Sequential(
            nn.Linear(in_features=1, out_features=1)
            )
  
  def forward(self, x):
    x = self.somelayer(x)
    return x

Understanding the Components

Extending nn.Module

class LinearRegressionModel(nn.Module): This line defines a new class called LinearRegressionModel that inherits from PyTorch’s nn.Module. In PyTorch, nn.Module is the base class for all neural network modules, which includes layers, or a collection of layers, that can process input data.

Initialization Method

def __init__(self): This is the initializer or constructor for our LinearRegressionModel class. It’s called when you create a new instance of this class.
super().__init__(): This line calls the initializer of the base class (nn.Module). This is necessary to properly initialize the underlying PyTorch machinery.

These parts for model construction should always be called. You always create a class with a desired name. Which needs an initializer and a initializer fore the base class (nn.Module). You could in theory always copy these.

The Layers

self.linearlayer = nn.Sequential(): This sets up a sequantial layer system, which means that PyTorch will arrange that any layers inside this sequential, feed to each other.

Inside this we have the neuron

nn.Linear(in_features=1, out_features=1: This is the neuron itself. This neuron needs two arguments, the in_features which represents the incoming connections. And the out_features which represents how many connections should go out of the neuron.

At the end we need to define the forward pass of the model. This tells PyTorch how we want the data to flow through the model.

def forward(self, x): This method defines how the input data x flows through the model. Whenever you make a prediction using the model, this method is automatically called.
x = self.linearlayer(x): This line is supposed to represent the processing of input x through a layer named linearlayer.
return x: This returns the output after passing the input data through the linear layer, completing the forward pass of the model.

In our case we will use a single neuron as fitting to a linear line is very easy. But if you would want to layers we would need to match both the out_features of the first and the `in_features’ of the second.

Like this:

self.linearlayer = nn.Sequential(
            nn.Linear(in_features=1, out_features=5), # note how we take one number in and five out.
            nn.Linear(in_features=5, out_features=1) # note how this layer MUST take in five numbers to match with the prior neuron
            )

Then we can use the model as such:

# setup a model
model = LinearRegressionModel()

# See model parameters
model.state_dict()

# pass data through the model
y = model(x)

🧮 Functions for Training

💸 The Loss (Cost) function

The loss function, often referred to as the cost function, is a critical component in training neural networks. It’s a method for evaluating how well your model’s predictions match the actual data. Essentially, the loss function measures the difference between the predicted values ($\hat{y}$) and the actual target values ($y$) across all instances in the training dataset. Or more simply worded, the loss function measures how wrong the model’s predictions are.

Both the predicted value and actual value are often reffered to in multiple ways.

Actual Value ($y$): The true value that corresponds to the model’s input. This is what the model aims to predict accurately.
Target: Often used interchangeably with actual value, it denotes the desired outcome the model is trained to predict.
Ground Truth: This term also indicates the actual value as a benchmark for model predictions.
Label: In supervised learning, each input feature set is associated with a label, which is the actual value the model is supposed to predict.

Purpose of the Loss Function

The main purpose of the loss function is to guide the training process. By quantifying the error of the model, it provides a clear objective for the optimization algorithms to minimize. In other words, the loss function tells the training algorithm how far off the predictions are from the actual results, and the algorithm then adjusts the model parameters (weights and biases) in a way that reduces this error.

Today we will work with:

nn.L1Loss() - Mean Absolute Error

For more on the loss functions, see: PyTorch nn.Loss documentation

Mean Absolute error tries to measure how far our predicted point is from the actual value. Visualizing this should show the intuition clearly.

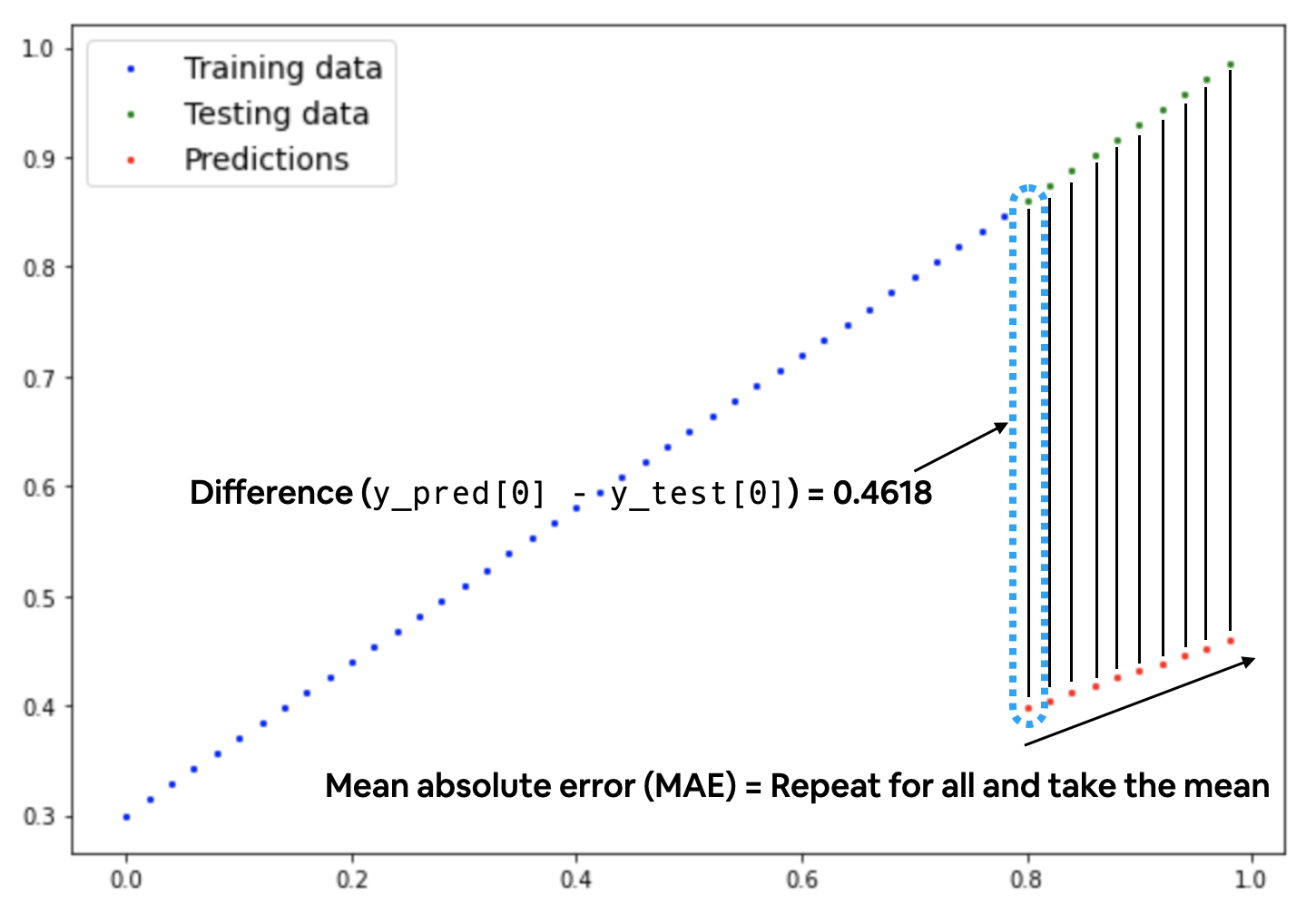
Mean Absolute error visualized — Figure 5: Mean Squared Error

🔥 Loss function in PyTorch

# Create loss function
loss_fn = nn.L1Loss()

🔧 The Optimizer

The optimizer is an algorithm or method used to change the parameters of the neural network, such as weights and learning rate, to reduce the losses. Optimizers are used to solve optimization problems by minimizing the loss function. Without the optimizer, we woulnd’t be able to change our network so it performs better.

This optimization process is highly intertwined with a concept known as backpropagation. Short for “backward propagation of errors,” backpropagation is a cornerstone algorithm in neural network training. Working hand-in-hand with optimizers, it adjusts the network’s weights based on the loss incurred during each training iteration. The essence of backpropagation is to iteratively reduce the loss by fine-tuning the network’s weights and biases, thereby minimizing prediction errors.

Imagine an artist refining a sketch: upon reviewing their work, if they notice discrepancies between their drawing and the subject, they make necessary corrections. Similarly, backpropagation evaluates the network’s output against the expected result. When it identifies a mismatch—the prediction error—it guides adjustments in the network’s internal settings to enhance future predictions.

Gradients: Charting the Path to Accuracy

Within this context of optimizing, you will often hear the term gradients. Gradients in neural networks are akin to the contours on a map, delineating the landscape’s rises and falls. In this analogy, these contours direct us towards areas of lower elevation, or reduced error. A gradient specifies the slope of our current position, indicating the direction in which the error’s descent is steepest. By following this path, marked by the gradient, we aim to reach the landscape’s lowest point, symbolizing the minimal error or the highest prediction accuracy of the network.

This interconnected system of optimizers, backpropagation, and gradients forms the backbone of neural network training. Through a cycle of evaluation, error measurement, and parameter adjustment, neural networks learn to improve their predictions, becoming increasingly adept at interpreting data and making accurate forecasts. This process not only refines the network’s performance but also underscores the intricate dance between mathematical principles and algorithmic strategies in the quest for artificial intelligence.

Learning Rate

There is one more important variable we need to set manually; the learning rate (LR). The learning rate determines the stepsize by which we try to descent. In the analogy of a landscape, it would be how large our steps are. Too small and we move towards the minimum slowly and might not make it out of larger gaps. Too large and we might skip the lowest point as we continue to step over it. Setting the right learning rate is difficult and often has a optimal value that differs per each problem. It is common to see some baseline learning rates like 0.1 for Stochastic Gradient Descent or 0.0003 for the Adam optimizer.

0.0003 (3e-4) is often referred to as the Karpathy constant claimed to be the most generalizable LR in conjuction with the adam optimizer.

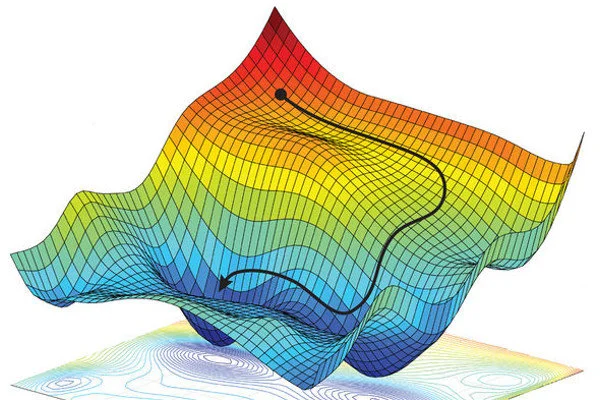
Gradient descent plotted out — Figure 6: Plotted line of how steps an optimizer might take during gradient descent. Source: Amini et al.¹

Note that in this image it is important to realize that the lower, the better.

The ‘height’ of the plot is represented by the loss fuctions value at those given parameters.

today we will make use of one of the most common optimizers in the field:

torch.optim.SGD() - Stochastic Gradient Descent (SGD)

For more on optimizers, see: PyTorch torch.optim documentation

🔥 Optimizer function in PyTorch

# Create optimizer
optimizer = torch.optim.SGD(params=model.parameters(),
                            lr=0.01)

🦾 Training a Network

The Training Loop

Forward pass - Train data through model
- The input data is fed through the model to generate predictions.
Calculate Loss
- The difference between the model’s predictions and the actual targets is computed using a loss function.
Optimizer zero grad (reset optimizer)
- Clears the gradients of all optimized tensors. This is necessary because gradients accumulate by default in PyTorch.
Loss backward (Backpropagation)
- Computes the gradient of the loss function with respect to the model parameters, indicating how the parameters should be adjusted to reduce the loss.
Optimizer step (adjust parameters)
- Updates the model parameters in the direction that minimizes the loss, based on the gradients computed in the previous step.
Repeat…

You would repeat the training loop numerous of times. This is because the network learns slowly and needs to converge to the lowest loss (gradient descent..) before it reaches its best performance. Often we try to stop when the loss no longer decreases. The amount of times you make a pass over the the full data is called an *epoch.

The Test (or validation) Loop

Forward pass - Test data through model
- The model makes predictions on the test dataset without adjusting its parameters.
Calculate Loss & Accuracy metrics
- The loss is calculated to gauge the model’s performance on the test data. Additionally, accuracy or other relevant metrics are computed to assess the model’s prediction accuracy.

🔥 Training in PyTorch

# Set the number of epochs (amount of times the model will pass over the data and attempt to learn)
epochs = 1000
# send model to the correct device (remember both data and model need to be on the same device)
model.to(device)

# Put data on the available device
# Without this, error will happen (not all model/data on device)
X_train = X_train.to(device)
X_test = X_test.to(device)
y_train = y_train.to(device)
y_test = y_test.to(device)

for epoch in range(epochs):
    ### Training
    model.train() # train mode is on by default after construction

    # 1. Forward pass
    y_pred = model(X_train)

    # 2. Calculate loss
    loss = loss_fn(y_pred, y_train)

    # 3. Zero grad optimizer
    optimizer.zero_grad()

    # 4. Loss backward
    loss.backward()

    # 5. Step the optimizer
    optimizer.step()

    ### Testing
    model.eval() 
    # put the model in evaluation mode for testing (inference)
    # 1. Forward pass
    with torch.inference_mode():
        test_pred = model(X_test)
    
        # 2. Calculate the loss
        test_loss = loss_fn(test_pred, y_test)

    # use % operator to see if fully divisable. 
    if epoch % 100 == 0:
        # reports per 100 epochs
        print(f"Epoch: {epoch:.2f} | Train loss: {loss:.2f} | Test loss: {test_loss:.2f}")

with this, you should be able to train your first model!

🆘 Debugging the issue from live-session

For those who attended the session live, we ended up debugging a bug for the last part of the session.

The bug was mainly caused by two underlying issues that I did not anticipate for properly:

Converting the pandas dataframe to a proper tensor needed some 🥷 brackets that were hard to spot.

❌

X = df['x'].to_numpy() 
y = df['y'].to_numpy()

✅

X = df[['x']].to_numpy() 
y = df[['y']].to_numpy()

We need the double brackets here. This is because otherwise pandas returns a series object. Converting a series object to numpy leads to a simple list. Converting a two columns leads to a list of lists structure (which we need).

The data generated by the datadrawer renders out without any interference to torch.float64. PyTorch by default operates on torch.float32.

after the split, we convert to tensors but need to ensure the dtype will be torch.float32 by passing as an argument.

❌

# Convert to tensors
X_train = torch.tensor(X_train)
X_test = torch.tensor(X_test)
y_train = torch.tensor(y_train)
y_test = torch.tensor(y_test)

✅

# Convert to tensors
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32)

Issue one comes in

📅 Next Session

Fitting to Non Linear data!

📚 Works Cited

Amini, Alexander, Ava Soleimany, Sertac Karaman, and Daniela Rus. “Spatial Uncertainty Sampling for End-to-End Control,” 2019. https://arxiv.org/abs/1805.04829.